Lineare Ungleichungssysteme (Polyeder) spielen in vielen schwierigen Problemen der Wirtschaft und Wissenschaften eine zentrale Rolle. In Rostock befassen wir uns mit der algorithmischen Ausnutzung von Symmetrien, die schwierige Computerrechnungen vereinfachen oder zukünftig überhaupt erst ermöglichen.
Arbeitsgruppe 'Geometrie'

Die Nachrichtenübermittlung kann man als eine Abbildung auf der Menge der 0/1-Folgen modellieren. Um die Kommunikation sicher gegen Kryptoangriffe zu gestalten, muss diese Abbildung gewisse Eigenschaften erfüllen. Oft werden die kryptographischen Abbildungen durch geschickte Ausnutzung von Eigenschaften eines endlichen Körpers konstruiert.
Arbeitsgruppe 'Diskrete Mathematik'

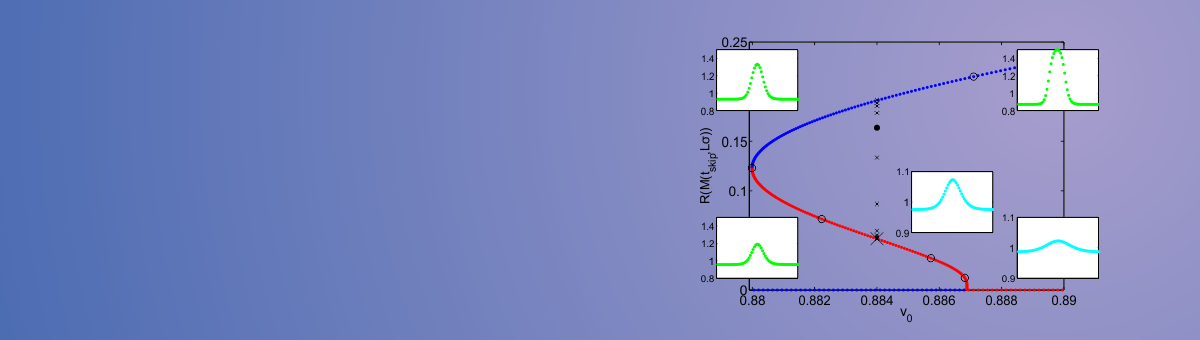
Große Systeme treten in vielen natur- und ingenieurwissenschaftlichen Anwendungen auf. Wir entwickeln numerische Methoden zur (Bifurkations-)Analyse des makroskopischen dynamischen Verhaltens dieser Systeme in Abhängigkeit relevanter Parameter. (Die Abbildung zeigt die Stauentstehung bei Verkehrsmodellen.)
Arbeitsgruppe 'Wissenschaftliches Rechnen'

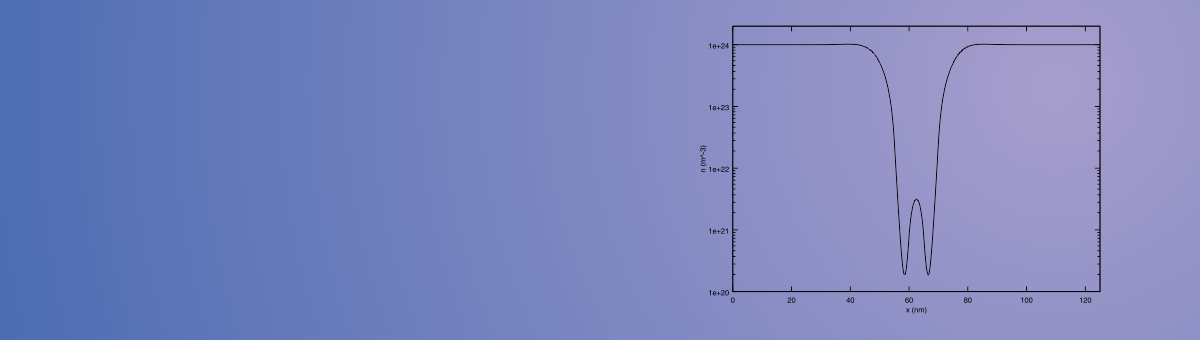
Viele Systeme aus Natur, den Wissenschaften und der Technik werden mathematisch durch Differentialgleichungen beschrieben. Wir untersuchen solche Gleichungen mit den Methoden der Analysis als Grundlage für ein besseres Verständnis ihrer Lösungen. Die Abbildung zeigt die Elektronendichte in einer Resonanztunneldiode.
Arbeitsgruppe 'Analysis-Differentialgleichungen'

Die Numerische Analysis beschäftigt sich unter anderem mit der Lösung gewöhnlicher und partieller Differentialgleichungen. Solche Gleichungen sind nur selten geschlossen lösbar. Eine numerische Approximation der Lösung gelingt etwa mit der Methode der finiten Elemente. Die Abbildung zeigt eine Eigenfunktion des Laplace-Operators auf einem Dreiviertelkreis.
Arbeitsgruppe 'Numerische Mathematik'

Sowohl in den Anwendungen als auch in der Theorie tritt die folgende Fragestellung in unterschiedlichsten Varianten auf, die vielfältige bekannte, aber auch noch zu entwickelnde Methoden zur Lösung erfordern: Für eine gegebene Funktion, die von vielen Veränderlichen abhängt, und für einen gegebenen Bereich, aus dem die Veränderlichen diskret oder kontinuierlich Werte annehmen dürfen, sind solche erlaubten Werte der Veränderlichen zu bestimmen, dass die Funktion einen maximalen bzw. minimalen Wert annimmt.
Arbeitsgruppe 'Mathematische Optimierung'

Zukunftstechnologie Künstliche Intelligenz: Maschinelles Lernen von Forschung bis Anwendung
Projekt 'Computational Intelligence Technology Lab'

Im Bereich der Mathematischen Statistik befassen wir uns mit Nichtparametrischer Statistik (z.B. Kurvenschätzung), asymptotischer Theorie statistischer Experimente (z.B. Le Cam-Äquivalenzen, Minimax-Raten, Adaptivität), statistischen inversen Problemen (z.B. Dekonvolution, Messfehlermodelle), Analyse funktionaler Daten und Zeitreihenanalyse.
Arbeitsgruppe 'Mathematische Statistik mit Schwerpunkt Stochastische Prozesse'

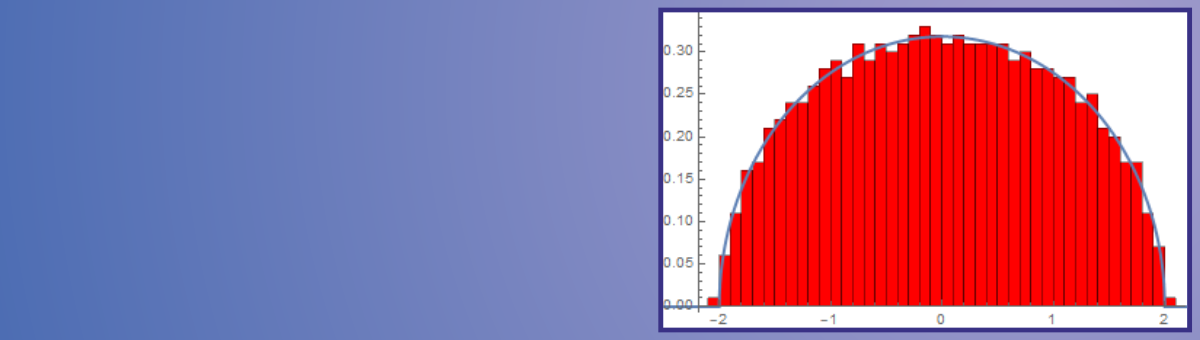
Stochastische Systeme treten in vielen Anwendungen in Natur, Technik und Wirtschaft auf. In der Wahrscheinlichkeitstheorie wird unter anderem untersucht, inwieweit das Verhalten solcher Systeme von den Eigenschaften seiner Komponenten abhängt.
Die Abbildung zeigt die Verteilung des Spektrums einer großen symmetrischen Zufallsmatrix.
Arbeitsgruppe 'Wahrscheinlichkeitstheorie'

Mathematik hat viele Gesichter — als Wissenschaft von Raum, Maß, Zeit und Abfolge, als Wissenschaft der Symbole, Strukturen und Muster, als Prototyp für wissenschaftliches Argumentieren, als Disziplin des Beweisens und Problemlösens. Eine zentrale Frage an Schnittstellen von Fachdidaktik, Mathematik, Philosophie, Soziologie und Lernpsychologie lautet, welche Rolle diese Gesichter für das Lehren und Lernen von Mathematik spielen können.
Arbeitsgruppe 'Didaktik der Mathematik'