Contents
Summer School - Mathematics of Data Sciences and Digitisation
The summer school deals with the mathematical background required for processing large amounts of data in connection with digitisation tasks. This includes lectures for data collection for bifurcation analysis of laboratory experiments, Functional Data Analysis, Nonparametric Curve Estimation, Page Rank Algorithm, Advanced Encryption Standard, Random Matrices and Machine Learning techniques.
Machine learning techniques
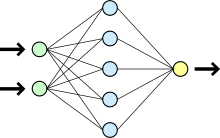
We will consider the basic methods for training and prediction with neural networks. Based on this, we will present different concepts for recursions. In addition, we will discuss Hidden Markov models and the Viterbi algorithm, which are also useful tools in machine learning.
Stochastics
Functional Data Analysis
In this lecture we study empirical data which cannot be represented by realizations of finite-dimensional random vectors but by realizations of random functions. Such data occur e.g. in medical statistics, meteorology and econometrics. We consider principal component analysis as a widely used procedure to represent and analyze such functional data. We consider estimators for the principal components.
Nonparametric Curve Estimation
We are dealing with the general question of how to estimate a probability density based on independent random variables from this density where one realization of each random variable is observed. Therein we do not impose any parametric assumption on the density, which determines the density up to finitely many real-valued parameters. We consider the kernel estimator and study its asymptotic properties. Moreover nonparametric regression problems are subject of the lecture.
Random Matrices and Data Science
In random matrix theory the statistical properties of the eigenvalues and the eigenvectors of large random matrices are investigated. In recent years the results and the techniques from random matrix theory have been applied to various problems from the field of data science, e.g. principal component analysis and deep networks.
The lecture will provide a brief introduction to random matrix theory as well as a glimpse of the recent applications to data science.
Numerics and Dynamics
Data collection for bifurcation analysis of laboratory experiments
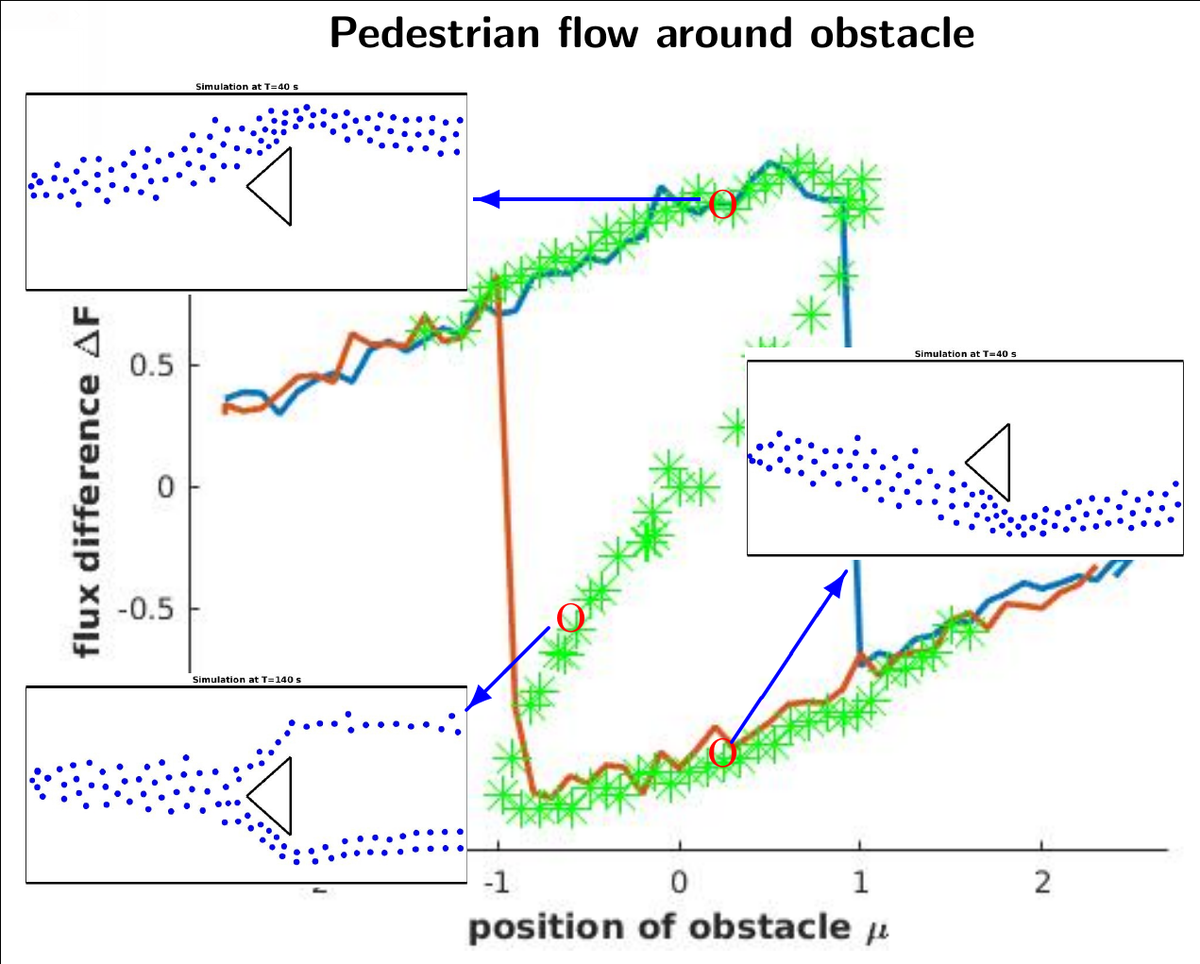
In contrast to the typical post-processesing in the context of data analysis the methods of control based continuation and equation-free bifurcation analysis allows to plan and evaluate measurements of laboratory experiments online to compute a bifurcation diagram directly from laboratory experiments. By this approach also unstable states of the experimment can be investigated which are not observable otherwise. This extends the information one can obtain from post-processing of experimental time-series. Examples will be given ranging from simple mechanical systems to pedestrian flows.
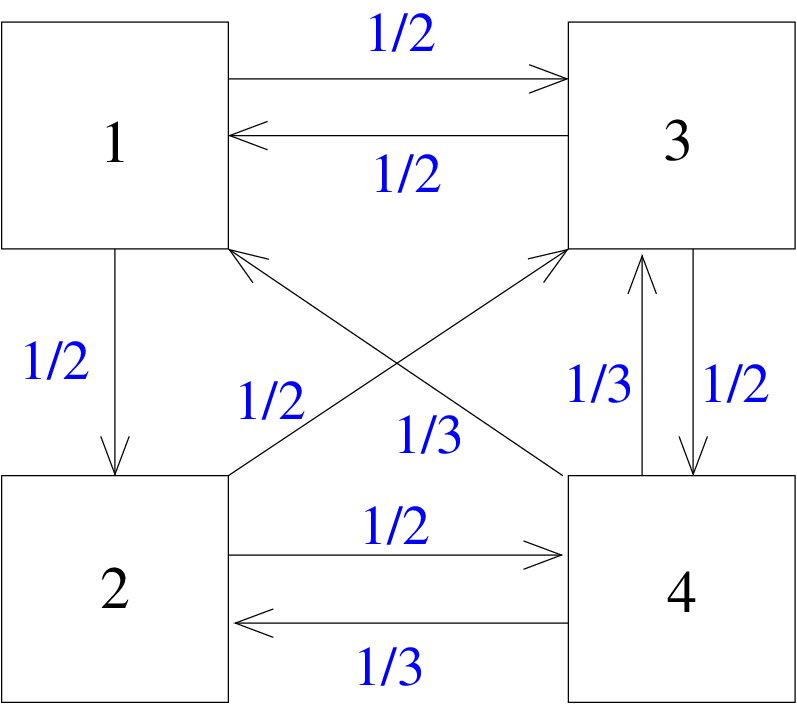
Matrix analysis, search engines and Google's PageRank
Numerical mathematics and numerical linear algebra are among the pillars of mathematical data sciences. A challenging field of application are methods for searching and ranking the web contents. This lecture introduces to some aspects of matrix analysis and matrix computations in order to explain basic ideas behind search engines as well as the ranking of search results by Google's PageRank algorithm.
AES: Advanced Encryption Standard
Cryptography ensures secure communication across networks like the internet. One of the most widely used cryptographic algorithms is the Advanced Encryption Standard (AES). The lecture gives a brief overview on the mathematical structure of AES.
The AES algorithm consists of linear and nonlinear components. After introducing the main ideas of the design of the nonlinear part, we will focus more specifically on the linear part. In particular, we present ideas on improving the speed of the AES algorithm that have been proposed very recently.